Teaching geometric constructions has always been a challenge. The rules are easy enough - compass, straightedge, no measuring. But for the teacher the challenges come quickly. How to actually demonstrate them in class? How will the students remember the steps when trying it themselves? What happens when they do the homework?
In the classroom
To demonstrate the constructions in class we have the usual choices:
Using a projector you can show each construction step by step while you discuss it with the class. The compass actually looks and acts like a compass, and it can draw partial arcs just the like the real one. The straightedge and pencil looks real also.

Stephen Corcoran, Head of Mathematics at St Stephen's School in Perth Australia reports after using the construction pages in the classroom:
The next problem arises when the students try to do it themselves. They have to rely on memory to redo what they saw a few minutes ago in class. This memory is typically not very good. Not until they have done it themselves a few times will they really retain it. The ultimate goal of course is to get to the point where the visual aid is no longer needed and they can perform the constructions in a test unaided. Using Math Open Reference, they can bring it up on a computer and follow along with the animations, pausing between steps. This leads to a high degree of success and hastens the time when they can do it unaided.
Some teachers do this in a computer lab setting while they walk around looking over shoulders to find the students who need some extra help. Teachers report that this activity is very engaging. According to Roy Chancellor, a math teacher in Scottsdale Arizona:
The third challenge arises when the students are at home. Once again, they have to recall what they saw in class and try and reconstruct the figures from memory. If they have trouble with this, the only recourse has been a written set of instructions, and these instructions are very hard to write - a bit like trying to describe how to tie shoelaces.
Because the Math Open Reference animations are freely accessible on the web without any special downloads or software, they can again see the step-by-step animations and practice at their own pace until they get it down. They are seeing the exact same animations they saw at school.
Software like GSP is less useful here because:
Constructions are taught as a fundamental part of a geometry curriculum, but they have other values. Some geometric concepts can seem a little abstract to some students. By linking them to physical constructions, the ideas become more concrete in the student's mind.
Again, Roy Chancellor:
It might be said that this is just rote "see and do", not real learning. But there is another view. Once the constructions have been practiced over and over and internalized, the training wheels can be cast aside. From that base of confidence, the discussion can be started into the real meaning of the constructions and the analysis of why they actually work.
Reference : www.mathopenref.com
In the classroom
To demonstrate the constructions in class we have the usual choices:
- Compasses and straightedge on a whiteboard or overhead projector.
- Software such as Geometers Sketchpad (GSP) or GeoGebra.
Using a projector you can show each construction step by step while you discuss it with the class. The compass actually looks and acts like a compass, and it can draw partial arcs just the like the real one. The straightedge and pencil looks real also.

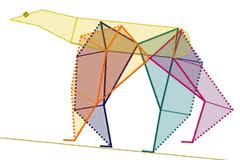
Fig 1. Freeze-frame of the angle bisection construction.
"The lesson was a huge success. Displaying your construction animations greatly increased student understanding, motivation and 10x more efficient. Also they can always visit your site themselves if they wish."
In the LabThe next problem arises when the students try to do it themselves. They have to rely on memory to redo what they saw a few minutes ago in class. This memory is typically not very good. Not until they have done it themselves a few times will they really retain it. The ultimate goal of course is to get to the point where the visual aid is no longer needed and they can perform the constructions in a test unaided. Using Math Open Reference, they can bring it up on a computer and follow along with the animations, pausing between steps. This leads to a high degree of success and hastens the time when they can do it unaided.
Some teachers do this in a computer lab setting while they walk around looking over shoulders to find the students who need some extra help. Teachers report that this activity is very engaging. According to Roy Chancellor, a math teacher in Scottsdale Arizona:
"Animated constructions are absolutely indispensable for guiding the students at their own pace. It would be next to impossible to teach these constructions in whole-group format. The students were engaged throughout the lab."
At Home The third challenge arises when the students are at home. Once again, they have to recall what they saw in class and try and reconstruct the figures from memory. If they have trouble with this, the only recourse has been a written set of instructions, and these instructions are very hard to write - a bit like trying to describe how to tie shoelaces.
Because the Math Open Reference animations are freely accessible on the web without any special downloads or software, they can again see the step-by-step animations and practice at their own pace until they get it down. They are seeing the exact same animations they saw at school.
Software like GSP is less useful here because:
- The student has probably not purchased it.
- The sketches do not show how they can be produced using real drawing instruments.
Constructions are taught as a fundamental part of a geometry curriculum, but they have other values. Some geometric concepts can seem a little abstract to some students. By linking them to physical constructions, the ideas become more concrete in the student's mind.
Again, Roy Chancellor:
"In my HS geometry class, we're doing a unit on properties of triangles, such as circumcenter, incenter, centroid, and orthocenter. After learning various theorems about these special locations, my students used your construction pages to create each one. After making the constructions, they used measuring tools to verify each of the theorems from earlier in the week. It was an excellent way to connect the book knowledge to something they created."
ConclusionIt might be said that this is just rote "see and do", not real learning. But there is another view. Once the constructions have been practiced over and over and internalized, the training wheels can be cast aside. From that base of confidence, the discussion can be started into the real meaning of the constructions and the analysis of why they actually work.
Reference : www.mathopenref.com




















0 comments:
Post a Comment